Dysprosium quantum gas microscope laboratory
We're developing an experiment to produce ultracold dipolar quantum gases of dysprosium atoms that can be manipulated and imaged under a high-resolution optical microscope.
Dipolar quantum gases represent a new frontier in cold-atom research. Atoms with a large magnetic dipole moment interact via the long-range, anisotropic dipole-dipole potential. In large collections of atoms, it is possible to create novel superfluids, supersolids and topological phases at ultracold temperatures.
Combined with the capabilities of a quantum gas microscope we aim to measure, understand and control both the bulk properties and microscopic correlations in these exotic many-body with single-atom resolution.
Our research projects
The quantum gas microscope is currently being constructed in a new laboratory for use by researchers across a broad selection of the Australian physics community and the ARC Centre of Excellence in Future Low-Energy Electronics Technologies.
Planned studies include:
- Exotic superfluidity in mixtures of two fermionic dysprosium isotopes with tunable interactions
- Dipolar gases in optical lattices — Bose and Fermi Hubbard systems with long-range interactions
- Driven and spin-orbit coupled atomic gases to investigate nonequilibrium and topological phenomena
- Sensing of magnetic fields using a novel ultracold source and the large Dy magnetic moment.
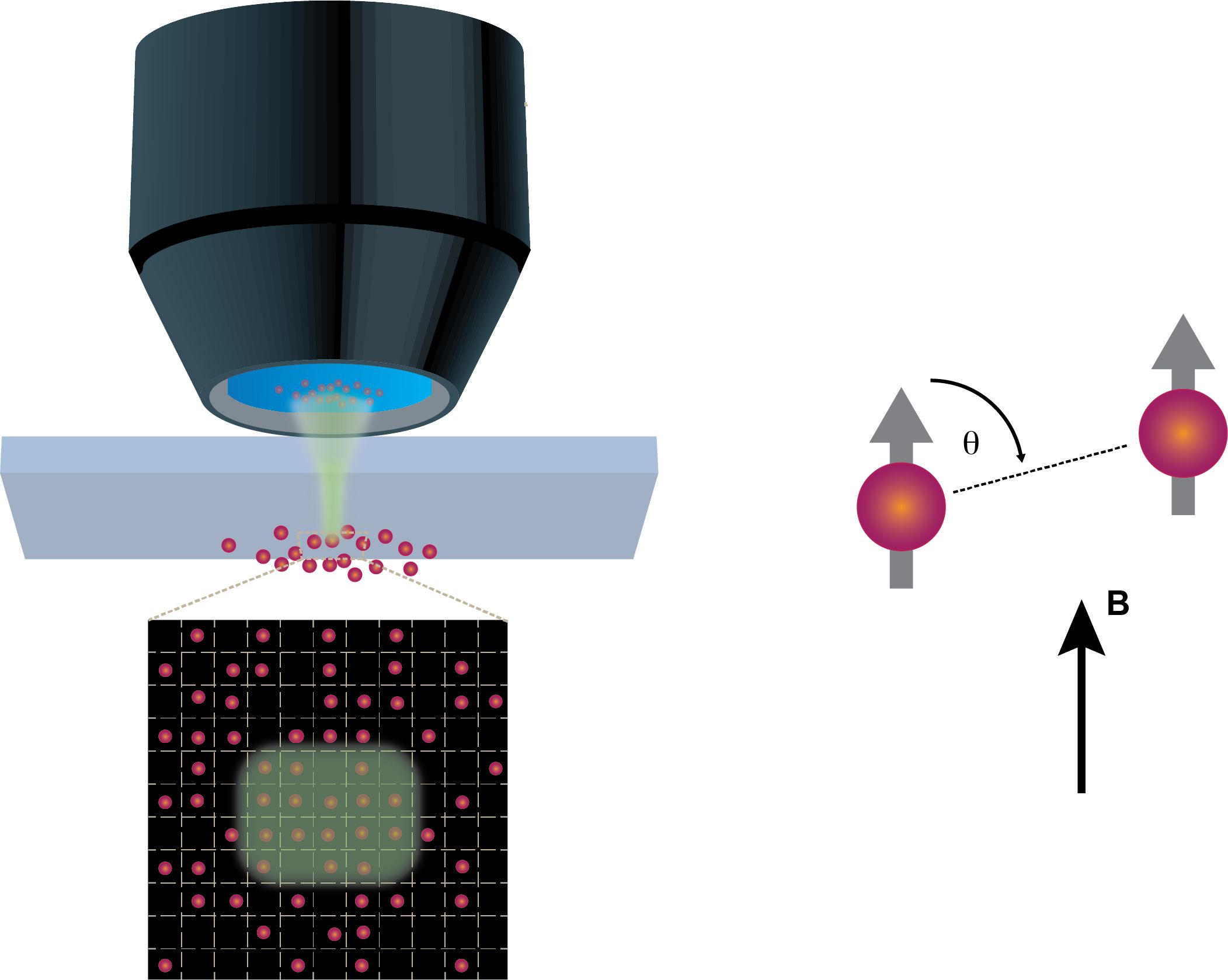
(Left) Principle of quantum gas microscopy. Ultracold atoms in an optical lattice can be imaged and controlled with single site resolution.
(Right) Ultracold dysprosium atoms experience the long-range dipole-dipole interaction which depends on the relative angle of the dipoles, aligned by an external magnetic field.
Our team
- Professor Chris Vale (group leader)
- Dr Sascha Hoinka (Postdoctoral Fellow)
- Dr Ivan Herrera Benzaquen (Postdoctoral Fellow)
- Dr Paul Dyke (Postdoctoral Fellow)
- Allan Pennings (PhD Student)
- Alex Armstrong (PhD Student)
Our partners
- Professor Andrei Sidorov (Swinburne)
- Professor Peter Hannaford (Swinburne)
- Professor Peter Drummond (Swinburne)
- Professor Andrew Truscott (ANU)
- Professor John Close (ANU)
- Associate Professor Nick Robins (ANU)
- Professor Kris Helmerson (Monash)
- Associate Professor Meera Parish (Monash)
- Dr Lincoln Turner (Monash)
- Dr Russell Anderson (La Trobe)
- Professor Matthew Davis (UQ)
- Professor Halina Rubinsztein-Dunlop (UQ)
- Professor Robert Scholten (Melbourne)
- Associate Professor Andrew Martin (Melbourne)
- Professor Tilman Pfau (Stuttgart)
Keen to be involved with our research?
We have openings for PhD, MSc and Honours students in the areas mentioned above. Please contact Professor Chris Vale directly for details or check out more project opportunities in other research areas.
Funding
- ARC LE180100142 – Universal few-to-many-body physics in 2D Fermi gases
- ARC CE170100039 – ARC Centre of Excellence in Future Low-Energy Electronics Technologies
Explore our other research programs
Contact the Optical Sciences Centre
There are many ways to engage with us. If your organisation is dealing with a complex problem, get in touch to discuss how we can work together to provide solutions. Call us on +61 3 9214 8096 or email osc@swinburne.edu.au.

