Time crystals with ultracold atoms
We conduct experimental and theoretical research in the emerging field of time crystals, which has potential long-term applications in quantum technologies. We provide research training in experimental and theoretical physics.
Time crystals (1), first proposed in 2012 by Physics Nobel Laureate Frank Wilczek, are systems that behave in the time dimension like ordinary space crystals do in space dimensions.
In 2015, Krzysztof Sacha from the Jagiellonian University in Krakow – a theory collaborator on this project – proposed that a periodically driven quantum many-body system can reveal spontaneous breaking of discrete time-translation symmetry and spontaneously start to evolve with a period longer than the driving period to create a time crystal.
Such a discrete time crystal is predicted to be robust against external perturbations and to persist for extremely long periods, in analogy with the behaviour of a normal space crystal.
When the interaction between atoms is sufficiently strong and attractive, periodically evolving states of the many-body system become Schrödinger cat-like superposition states, so that an infinitesimally small perturbation is sufficient to break the time-translation symmetry and collapse the system into one of the multiple evolving wave-packets.
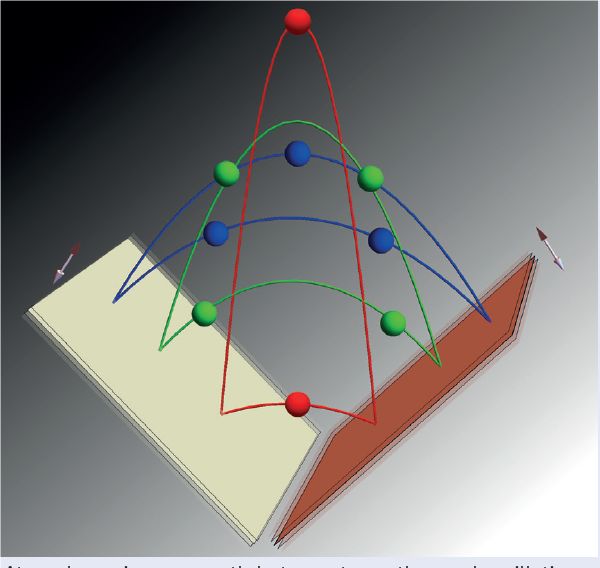
We have set up an experiment to create a discrete time crystal based on a Bose-Einstein condensate of ultracold potassium-39 atoms bouncing resonantly on an oscillating atom mirror such that the bounce period equals an integer multiple of the mirror oscillation period (2, 3).
Potassium-39 is chosen as the atomic system because it has a broad magnetically tuneable Feshbach resonance (at 402 G), which allows the interaction between the atoms to be tuned very precisely.
An important characteristic of such a ‘gravitational bouncer’ system, compared with, for example, spin-based systems, is accessibility to dramatic breaking of time-translation symmetry with an evolving period that can be orders of magnitude longer than the driving period (2).

Such ‘big time crystals’ can involve up to about 100 temporal lattice sites and are suitable for implementing a broad range of condensed matter phenomena in the time domain (2, 4, 5) such as:
- Anderson localization and many-body localization with temporal disorder
- Mott insulator phases in the time domain
- topological time crystals, involving edge states in time
- time crystals with exotic long-range interactions
- two-dimensional time crystals involving ultracold atoms bouncing between two oscillating mirrors
- time quasi-crystals, ordered but not periodic in time
- ‘time-tronics’ involving temporal semiconductor-like devices and memory devices for storage of information in the time dimension.
Together with our theory collaborators, we are also conducting research into the fundamental principles underlying time crystals and their applications (6, 7, 8).
- P. Hannaford and K. Sacha, A decade of time crystals: quo vadis, European Physics Letters 139, 10001 (2022).
- K. Giergiel, A. Kosior, P. Hannaford and K. Sacha, Time crystals: analysis of experimental conditions, Physical Review A 98, 013613 (2018).
- K. Giergiel, T. Tran, A. Zaheer, A. Singh, A. Sidorov, K. Sacha and P. Hannaford, Creating big time crystals with ultracold atoms, New Journal of Physics 22, 085004 (2020).
- P. Hannaford and K. Sacha, Time crystals enter the real world of condensed matter, Physics World 33, 42-46 (2020).
- P. Hannaford and K. Sacha, Condensed matter physics in big discrete time crystals, AAPPS Bulletin 32, 12 (2022).
- J. Wang, P. Hannaford and B. J. Dalton, Many body effects and quantum fluctuations for discrete time crystals in Bose-Einstein condensates, New Journal of Physics 23, 063012 (2021).
- J. Wang, K. Sacha, P. Hannaford and B. J. Dalton, Discrete time crystals in Bose-Einstein condensates and symmetry-breaking edge in a simple two-mode theory, Physical Review A 104, 053327 (2021).
- K. Giergiel, J. Wang, B. J. Dalton, P. Hannaford and K. Sacha, Discrete time crystals with absolute stability, Physical Review B 108, L180201 (2023).
Experimental team
| Name | Position |
|---|---|
| Professor Peter Hannaford | Leader |
| Professor Andrei Sidorov | |
| Dr Ali Zaheer | Research Fellow |
| Arpana Singh | PhD student |
| Chamali Gunawardana | PhD student |
| Mohammed Bouras | PhD student |

Experimental time crystal team (left to right): Arpana Singh, Peter Hannaford, Ali Zaheer, Satoshi Tojo, Chamali Gunawardana and Andrei Sidorov.
Theory collaborators
| Name | Affiliation |
|---|---|
| Professor Krzysztof Sacha | Jagiellonian University, Krakow, Poland |
| Dr Krzysztof Giergiel | CSIRO, Melbourne, Australia |
| Professor Bryan Dalton | Swinburne University of Technology, Melbourne, Australia |
| Associate Professor Hui Hu | Swinburne University of Technology, Melbourne, Australia |
| Dr Jia Wang | Swinburne University of Technology, Melbourne, Australia |
Visiting researchers
| Name | Affiliation |
|---|---|
| Professor Satoshi Tojo | Chuo University, Tokyo, Japan (2021–2022) |
| Dr Krzysztof Giergiel | Jagiellonian University, Krakow, Poland (2022–2023) |
| Professor Krzysztof Sacha | Jagiellonian University, Krakow, Poland (2024) |
Past members
| Name | Position |
|---|---|
| Dr Tien Tran | Postdoctoral Fellow |
Like to be involved with our research?
Honours and PhD projects are available. Contact Professor Peter Hannaford to discuss further details or check out more project opportunities in other research areas.
Funding information
- ARC Discovery grant: DP190100815 (2019 to 2023)
- ARC Discovery grant: DP240101590 (2024 to 2026)
Explore our other research programs
Contact the Optical Sciences Centre
There are many ways to engage with us. If your organisation is dealing with a complex problem, get in touch to discuss how we can work together to provide solutions. Call us on +61 3 9214 8096 or email osc@swinburne.edu.au.

